When a series of numbers contains no recognizable patterns, it is known as random numbers. Random numbers are the concept that is widely used in Statistics. In Statistics, to assure that the study is conducted without bias, random numbers are frequently used while picking random samples. However, picking random numbers manually can be quite difficult. To overcome this problem, we can simply use the RAND or RANDBETWEEN function to generate Random numbers in Google Sheets. In this article, we will understand everything about how to generate random numbers with the help of Google Sheets Tips. Read further to find more.
|
Table of Contents |
How to Generate Random Numbers in Google Sheets in RANDBETWEEN Functions?
To generate the random numbers in spreadsheets, we will have to use the RANDBETWEEN syntax. In this example, we will generate random numbers between the range of 1 to 10. The steps to get this done in Google Sheets are as follows:
- 1st Step: Open the Google Spreadsheet on your device.
- 2nd Step: Now on the homepage, move to the cell where you want to find the random numbers in between the lower limit or upper limit.
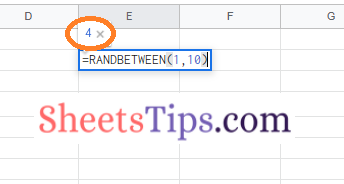
- 3rd Step: Simply use the formula =RANDBETWEEN(1,10).
- 4th Step: Now press the “Enter” button.
Now this will display random numbers between 1 to 10 as shown in the image given below.
- How to Convert Formula to Value in Google Sheets?
- Concatenate in Google Sheets: Concatenate Multiple Cells using Separator, Comma
- The Ultimate Guide to Using Conditional Formatting in Google Sheets
How To Generate Random Numbers in Google Spreadsheet for a Cell Range?
In the previous section, we use the random number function and entered the default value. Now in this section, lets us find how to generate the random numbers in the cell range by following the steps as given below:
- 1st Step: Launch the Google Spreadsheet on your device.
- 2nd Step: Now on the homepage, click on the cell where you want to find the random numbers between two cells. In our example, we are using cell D2.
- 3rd Step: Enter the formula as =RANDBETWEEN(A2, B2).
- 4th Step: Press the Return Key and now you will find the results as shown in the image given below.

It is important for you to note that the RANDBETWEEN functions are really helpful when you want a large range of numbers. For example, if you want to generate random numbers between 10 to 1000, then we can simply use the RANDBETWEEN functions.
Also, the RANDBETWEEN function is useful only if you want to generate random numbers in integers. If you are using decimal numbers then RANDBETWEEN will not be helpful. To overcome these issues, we can simply replace RANDBETWEEN functions with RAND function.
How To Generate Random Numbers in Google Spreadsheet using RAND Function?
The steps to find the random number in Google Sheets using RAND functions are as follows:
- 1st Step: Open the Google Spreadsheet on your device.
- 2nd Step: Now on the homepage, move to the cell where you want to find random decimals between two numbers.
- 3rd Step: Use the formula =RAND() and press the “Enter” button.
Now you will see the Random numbers being generated on the screen.
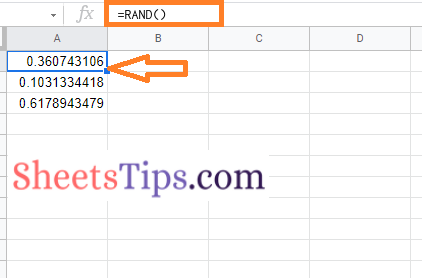
You will be noticing that the decimal numbers generated here on the screen are quite big. To roundoff the Random decimal numbers generated you can simply follow the steps as outlined below:
- 1st Step: Open the Google Sheets on your device.
- 2nd Step: Here on the homepage, move to the cell where you want to find the random decimal numbers in the roundoff manner.
- 3rd Step: Simply use the formula =Round(RAND(),3).
- 4th Step: Press the Enter key and you will see the results as shown below.
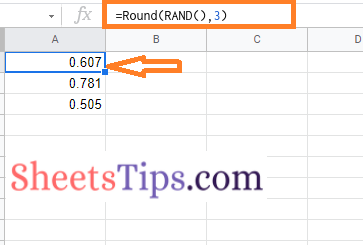
Since we have mentioned 3, it will show 3 decimal point numbers. If you use 2, you will be shown two decimal places. Thus you can customize this formula as per your needs.
How To Generate Random Numbers in Google Sheets without Duplicates?
We can simply use the RAND function or RANDBETWEEN function to generate the numbers in Google Spreadsheet without repeating. The steps to generate the random numbers in Google Spreadsheet without using the duplicates are as follows:
- 1st Step: Open the Google Spreadsheet.
- 2nd Step: Now move to the cell where you want to generate the random numbers.
- 3rd Step: Type the formula =RAND() * (10 – 1) + 1 or =RANDBETWEEN(1,1000).
- 4th Step: Press the “Enter” key and you will see the results as shown below.
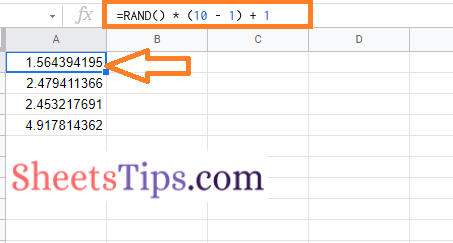
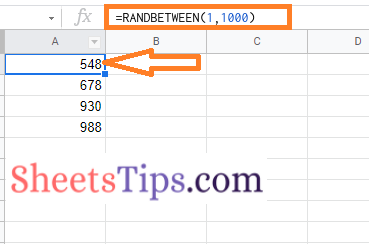
Now drag the formula applied cell using the fill handle and you will see the random numbers being generated without any duplicates.
